
Знаменитый математический спор: почему выражение 6:2(1+2) до сих пор вызывает разногласия
Наверняка вы хотя бы раз встречали задачу, которая на первый взгляд выглядит элементарно, но при этом умудряется рассорить людей с математическим образованием. Речь идёт о выражении 6:2(1+2). Одни уверенно заявляют, что ответ равен 1, другие не менее уверенно настаивают на результате 9. И самое интересное — обе стороны приводят логичные аргументы.
Почему простая запись превращается в повод для споров
На первый взгляд кажется, что проблема в незнании школьных правил. Однако на самом деле корень конфликта гораздо глубже. Подобные задачи чаще всего не являются реальными примерами из учебников. Они специально создаются для того, чтобы продемонстрировать важную особенность математики — неоднозначность записи при нарушении правил математической нотации.
Контекст решает всё: один символ — разные смыслы
В математике одна и та же запись может интерпретироваться по-разному в зависимости от контекста. Например, запись 2 3/4 мы сразу воспринимаем как смешанное число. Но если написать 2y/4, то очевидно, что это уже выражение с переменной, а не число. Формально записи похожи, но смысл у них принципиально разный.
Вот хороший пример.
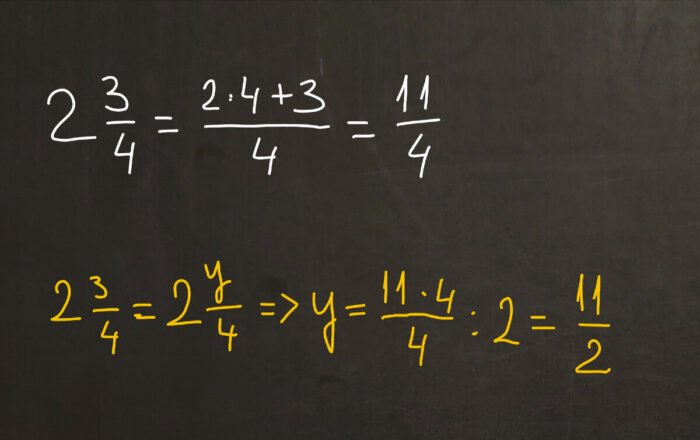
Тригонометрия как источник формальных неточностей
Ещё один наглядный пример — тригонометрические функции. Формально запись sin²x вовсе не означает sin(x²), а тем более sin(sin(x)). Тем не менее все без исключения понимают, что речь идёт о квадрате синуса аргумента x. Аналогично запись sin2x всегда читается как sin(2x), хотя строгая формальная логика могла бы предложить иную интерпретацию.
Школьные правила и реальная практика вычислений
В начальной школе нас учат, что умножение и деление имеют одинаковый приоритет и выполняются слева направо. При этом нигде официально не закреплено правило, что пропущенный знак умножения имеет преимущество над делением. Однако на практике многие учебники и примеры косвенно намекают именно на такую трактовку.
Пример из школьных учебников
В учебниках можно встретить выражения вида 14a²b²:a²b², где результат очевидно равен 14b. Если бы мы строго следовали правилу «слева направо» без приоритета неявного умножения, результат оказался бы совершенно другим. Это показывает, что даже в официальных источниках используется контекстное понимание записи.
Физика и инженерия: никакой двусмысленности
В физике подобные вопросы обычно не возникают. Запись 2mgh:2gh однозначно воспринимается как деление всего числителя на весь знаменатель. Чаще всего для этого используют дробную черту, что полностью исключает возможность двойного толкования. Именно поэтому инженеры и физики редко попадают в подобные ловушки.
Что говорят типографские стандарты и ГОСТ
Согласно типографским стандартам, умножение рекомендуется обозначать точкой или знаком «×». Запись без знака умножения допускается только в том случае, если смысл выражения абсолютно ясен всем читателям. Это ключевой момент. В выражении 6:2(1+2) такой однозначности нет, а значит запись считается некорректной.
Так какой же ответ правильный?
Строго говоря, правильного ответа здесь не существует. Всё зависит от того, какую интерпретацию вы выбираете. Именно поэтому подобные задачи — не про математику, а про внимательность к записи и умение ясно формулировать мысли. Автор выражения либо сознательно хотел запутать читателей, либо пренебрёг важным принципом однозначности.
Почему математика допускает такие упрощения
Несмотря на репутацию максимально точной науки, математика полна условностей и сокращений. Причина проста — удобство. Если бы мы всегда писали выражения строго формально, любая формула выглядела бы громоздко и трудночитаемо. Например, основное тригонометрическое тождество пришлось бы записывать как (sin(x))²+(cos(x))²=1, что значительно менее удобно.
Главный вывод, который стоит запомнить
История с выражением 6:2(1+2) учит нас не искать «хитрые» ответы, а стремиться к ясности. В математике, как и в жизни, крайне важно быть понятым однозначно. Именно поэтому рекомендуется избегать сложных и двусмысленных записей, особенно если их будут читать другие люди.
Поделитесь статьёй и оставайтесь с нами
Если материал оказался полезным и заставил взглянуть на математику под новым углом — обязательно поделитесь этой статьёй с друзьями. Подписывайтесь на обновления, чтобы не пропускать интересные разборы, логические задачи и неожиданные факты из мира науки.
ПОДПИСЫВАЙТЕСЬ на наш Канал в Телеграм – https://t.me/alibabainfo и регулярно получайте тематические новости, статьи, фото, видео и много другой информации.






